고정 헤더 영역
상세 컨텐츠
본문
이번 블로그에서는 이진 탐색(Binary Search)에 대해 알라보도록 하자.
이 이진탐색은 한번 비교를 거칠때 탐색 범위가 반(1/2)으로 출어들기 때문에 탐색 속도가 매우 빠르다.
하지만 이 탐색기법은 정렬된 배열을 전제로 하는 한계점을 가지로 있다.
그러므로, 이진 탐색을 사용할때는 배열이 정렬되 있는 상태거나 배열 정렬 시 발생되는 소요시간이 많지 않은 상황에서 사용하는 것이 좋다.
이진 탐색(Binary Search)의 탐색 과정

이제 한번, 위같은 정렬된 배열에서 이진 탐색(Binary Search) 알고리즘을 적용했을때 어떠한 과정을 거치는지 함께 살펴보도록 합시다. 위의 데이터 집합에서 8이란 데이터를 탐색하도록 하겠습니다. 자, 우선 첫번째 과정으로는 데이터 집합의 중앙 요소를 선택합니다.
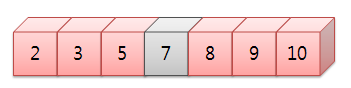
두번째 과정으로는 중앙 요소의 값과 찾으려는 값을 서로 비교하게 되는데, 만약 찾으려는 값이 중앙 요소의 값보다 작다면 중앙 요소의 왼편에서 중앙 요소를 다시 택하고, 반대로 찾으려는 값이 중앙 요소의 값보다 크다면 오른편에서 중앙 요소를 다시 택하게 됩니다. 그리고 다시 이진 탐색(Binary Search)를 거치는 것입니다. 위의 경우에는 찾으려는 값인 8이 중앙값 7보다 크므로 중앙값 왼편에 있는 데이터와 비교할 필요가 없는거겠죠? 중앙 요소 오른편에서 중앙값을 다시 택합니다.

이제는 중앙값이 9이고, 다시 중앙값과 찾으려는 값을 다시 비교하게 됩니다. 찾으려는 값 8은 중앙값 9보다 작으므로 중앙값 왼편에서 데이터를 찾아야 하겠네요?
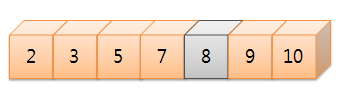
그럼 다시 왼편에서 중앙값을 선택합니다. 그렇게 되면, 남은 데이터 8이 중앙값으로 택해지게 되는데 찾으려는 데이터와 일치하므로 탐색을 끝마칩니다.
이진 탐색(Binary Search)의 성능
이진 탐색의 과정을 봐보니 상당히 빨라보이죠? 이러한 이진 탐색 알고리즘의 성능은 어떨까요? 한번 비교가 이루어질때마다, 범위는 1/2로 줄어든다고 했었습니다. 위의 데이터 집합의 크기를 n으로 두고, 반복 횟수를 k로 둔다면 아래와 같은 수식이 만들어집니다.

즉, 이진 탐색은 O(logN)의 속도를 보장합니다.
이진 탐색(Binary Search)의 구현
아래는 이진 탐색 알고리즘을 어떻게 구현해야 하는지 보여줍니다.

위 함수에서의 low는 탐색 범위에서 가장 왼쪽의 요소의 위치고, high는 탐색 범위에서 가장 오른쪽 요소의 위치를 나타냅니다. 그리고 mid는 그 탐색 범위의 중앙값을 나타냅니다. 각 줄에 대한 설명은 주석으로 달아놨으니 참고하시고, 위의 함수를 사용하여 어떠한 데이터 집합에서 특정 값을 찾는 예제를 보여드리도록 하겠습니다.



위의 예제를 살펴보시면, 무한 루프를 돌면서 사용자에게 입력을 요구합니다. 입력된 input 값에 따라, 이진 탐색 알고리즘을 통하여 찾으려는 데이터가 몇번째 요소인지 알려주는 예제라고 할 수 있습니다.
'Data Structure & Algorithm' 카테고리의 다른 글
| 탐욕 알고리즘(Greedy Algorithm) (0) | 2023.05.22 |
|---|---|
| 백트래킹(Backtracking) 알고리즘 (0) | 2023.05.21 |
| 합병 정렬(Merge sort) (0) | 2019.08.25 |
| 삽입 정렬(Insertion sort) (0) | 2019.08.23 |
| 선택 정렬(selection sort) (0) | 2019.08.21 |





댓글 영역